Mickaël D. Chekroun

Researcher

Ph. D in Mathematics
mchekroun@atmos.ucla.edu

Research Interests

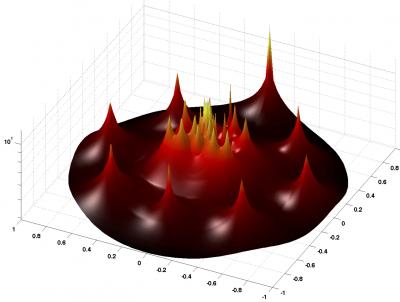
Modes of Variability: 

• Kolmogorov modes of jump-diffusion models
• Data-adaptive harmonic modes
• Ruelle-Pollicott resonances, correlations and power spectra
• Characterization of stochastic nonlinear oscillations

Stochastic Non-equilibrium Systems: 

• Non-Markovian reduced models to unravel transitions
• Stochastic transitions in non-equilibrium systems
• Stochastic invariant manifolds for SPDEs
• Stampacchia Maximum Principle for SPDEs

Data-driven Equations Discovery:

• Data-driven stochastic models and the Koopman operator
• Data-driven networks of stochastic nonlinear oscillators
• Data-driven non-Markovian closure models

Closure of Multiscale Systems:

• Non-Markovian reduced models to unravel transitions
• Anticipating tipping points and higher-order critical transitions
• Variational approach to closure of nonlinear dynamics
• Fast oscillations and balance motions in reduced primitive equations
• Stochastic rectification of slow manifold closures
• Stochastic nonlinear oscillator models of  jet-eddy interactions 

Response Theory/Optimal Control: 

• Linear response of jump-diffusion models
• Jump-diffusion induced chaos in high-dimension
• Detecting and attributing change in climate and complex systems
• Rough parameter dependence and Ruelle-Pollicott resonances
• Finite-horizon parametrizing manifolds for optimal control reduction

Time-Delay Systems: 

• Shear-induced chaos and model’s variability enhancement
• SNO bifurcation, tipping solution paths, and ENSO variability
• Hopf bifurcations in cloud-rain delay models
• Galerkin-Koornwinder approximations
• Optimal control of delay equations

Machine Learning for Complex Systems:

• Turbulence closure with small, local neural networks
• The high-frequency and rare events barriers to neural closures

Critical Transitions:

• Non-Markovian reduced models to unravel transitions
• Stochastic transitions in non-equilibrium systems
• Anticipating tipping points and higher-order critical transitions
• Pullback Attractor Crisis

Applications to Earth Science (selected): 

• Detecting and attributing change in climate and complex systems
• Gibbs states and Brownian models for haze and cloud droplets
• Theoretical tools for climate crisis and Hasselmann’s program revisited
• Opposing trends of cloud coverage over land and ocean
• Past-noise forecasting of ENSO
• Data-driven stochastic modeling of Arctic sea ice
• Low-order reduced models of GCM datasets
• Low-order reduced models of Madden-Julian oscillation
• Paleoclimate stochastic models
• Stochastic climate dynamics and random attractors

Turbulence Closure with Small, Neural Networks:

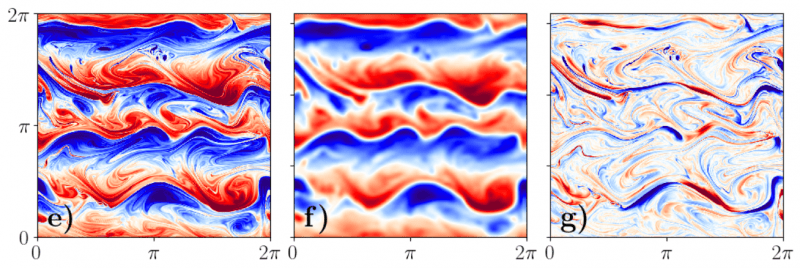
Vimeo movie: https://vimeo.com/824681438

Stochastic Strange Attractor (Chekroun et al. (2011), Physica D, 240):

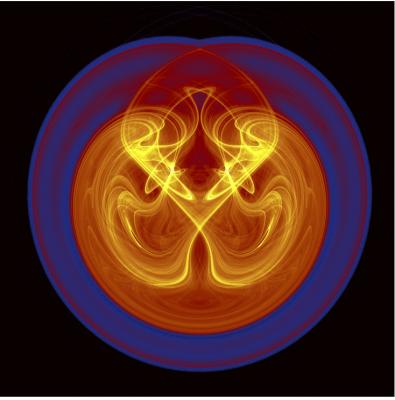
Vimeo movie: https://vimeo.com/240039610

Cloud Physics and Stochastic Strange Attractors (Chekroun et al. (2022), Science Advances, 8 (46)):

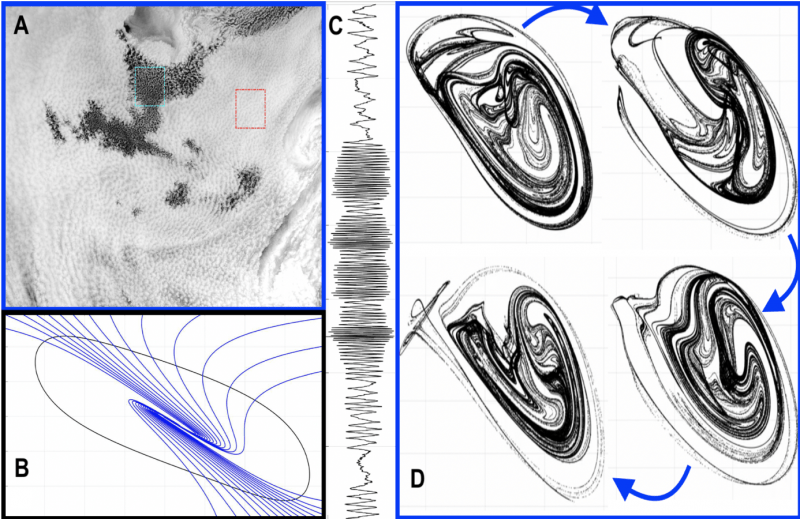
Vimeo movie: https://vimeo.com/773696444